Начертательная геометрия изучает способы построения изображений предметов на плоскости и обеспечивает исследование свойств предмета по его изображениям. Изображение предмета на плоскости называется чертежом. К чертежу предъявляются требования наглядности и обратимости, то есть возможности дать полное представление о предмете и возможности перейти от изображения на плоскости к его пространственному представлению.
Основным методом построения изображений является метод проекций. Для осуществления проецирования необходимо иметь:
- источник проецирующих лучей — точку S и источник проецирующих лучей l,
- объект проецирования — точку A, примитив, из которого состоят все геометрические образы (прямые, плоскости, поверхности),
- плоскость проекций H или V.
Проекцией точки будем считать точку пересечения проецирующего луча, проходящего через точку A с плоскостью проекций: горизонтальной — H или фронтальной — V (рис. 1).
В зависимости от положения точки S проецирование может быть
1) центральным, когда точка S (xS, yS, zS) — точка собственная; или
2) параллельным, когда точка S удалена в бесконечность и все лучи, практически, стали параллельными.
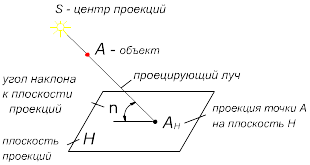
Рис.1 – Построение проекции точки
В зависимости от угла φ — встречи проецирующего луча и плоскости проекций — проекции могут быть косоугольными, при φ ≠ 90° и прямоугольными (ортогональными), при φ = 90°.
Для построения технических чертежей используется параллельное ортогональное проецирование.
Основоположником такого способа построения чертежа (эпюра) был Гаспар Монж, видный ученый и политический деятель 18 и начала 19 вв.
Проекции объекта проецирования — точки A — строят на две взаимно перпендикулярные плоскости проекции — горизонтальную H и фронтальную V. Для построения проекций точки в Евклидовом пространстве необходимы три координаты точки x, y, z. Линия пересечения горизонтальной и фронтальной плоскости проекций есть ось x, располагается горизонтально. Начало отсчета координаты x — справа у начала оси x, ось у направлена на наблюдателя, ось z — вертикально вверх (рис. 2).
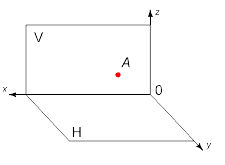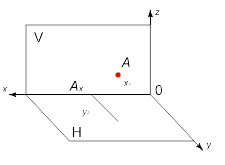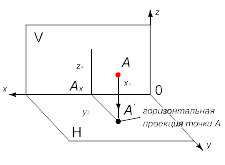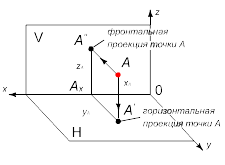
Рис. 2 – Проекция точки в Евклидовом пространстве на две плоскости проекций
При проецировании на две взаимно перпендикулярные плоскости проекций из точки A пространства опускают два перпендикуляра: один на плоскость H, а другой — на плоскость проекций V. В точках пересечения перпендикуляров с плоскостями проекций получаем горизонтальную проекцию A’ и фронтальную проекцию A’’. Две проекции точки A(A’,A’’) вполне определяют ее положение в пространстве.
Развернув горизонтальную плоскость проекций относительно оси x до совмещения с фронтальной плоскостью, получаем плоский чертеж с двумя проекциями A’ и A’’точки A.
Проекции проецирующих лучей из точки A пространства, проведенных до плоскостей проекций H и V, образуют линию связи между A’ и A’’, перпендикулярную оси x (рис. 3).
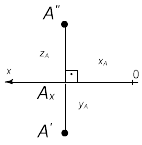
Рис. 3 – Эпюр точки в плоскостях H и V
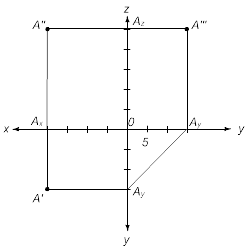
Точка. Построение 3-х проекций точки на плоскостях H, V и W
Задача.
Дано: A(20,15,25)
Построить A', A'', A'''
Решение:
1) строим оси проекций x, y, z на плоском чертеже. Сначала ось x-o отмечаем т. O и строим перпендикулярные оси x - оси z и y.
2) Выбираем масштаб 5 мм. Откладываем координату x=20мм. Отмечаем Ax по оси x. Затем координату y=15 и отмечаем точку Ay на оси y. На пересечении отрезков x20y15 находим A'.
3) Откладываем координату z=25мм и находим точку Az на оси z. На пересечении линии связи от A'Ax и линии связи OAz||OAx находим A''.
4) Продлили линию A''Az до пересечения с AyA'''. Получили A'''.