Известно, что натуральную величину плоскости можно определить, расположив ее параллельно плоскости проекций.
Это достигается в данном случае вращением плоскости фигуры относительно горизонтали (или фронтали). Каждая вершина вращающейся плоскости движется по окружности, плоскость которой перпендикулярна оси вращения. Если построить натуральную величину радиуса вращения вершины, то плоскость фигуры можно считать плоскостью параллельной плоскости проекций и определять ее натуральную величину.
Задача: определить натуральную величину плоской фигуры.
Дано: ɖ(∆ABC)
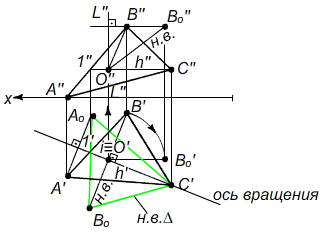
Рис. 8. – Построение натуральной величины плоской фигуры способом вращения вокруг горизонтали плоскости
Алгоритм решения:
Данная задача сводится к определению натуральной величины радиуса вращения одной из вершин треугольника относительно оси вращения h' (горизонтальной проекции горизонтали).
1) Строим проекции горизонтали плоскости h''(C''1'') и h'(C'1').
2) Из т.В перпендикулярно h' (см. Теорему о проецировании прямого угла) строим радиус вращения B'O' и его фронтальную проекцию B''O''.
3) Определяем натуральную величину радиуса вращения ob (O'B', O''B'') способом вращения вокруг фиксированной оси i (можно и другими способами). (11) Это отрезок прямой O''Bo''.
4) На горизонтальной проекции треугольника от точки O' (на продолжении радиуса вращения O'B') откладываем натуральную величину радиуса вращения O'Bo'. Отмечаем точку Bo, принадлежащую натуральной величине плоскости треугольника.
5) Другая вершина треугольника C' принадлежит оси вращения h', а, значит, и натуральной величине плоскости треугольника. C'≡Co
6) Вершину Ао находим следующим образом:
Известно, что точка А будет вращаться в плоскости, перпендикулярной оси вращения h', потому от т. A' троим перпендикуляр к h'. В то же время т. Ao должна находиться на стороне треугольника ab - прямой Bo1'Ao. Находим т. Ао на пересечении Bo1'Ao с перпендикуляром, проведенным от т. Ао. Соединив вершины C', Bo, Ao, получим искомую натуральную величину плоскости треугольника.

