(7) Из перечисленных выше методов рассмотрим б) вращение вокруг проецирующей фиксированной оси и в) вращение вокруг линии уровня плоскости – горизонтали либо фронтали ее. Остальное предлагаем учащимся для самостоятельного знакомства.
Сущность методов вращения:
1) Плоскости проекций не меняют своего положения
2) Частное положение относительно плоскостей проекций могут занимать геометрические образы (прямые, плоскости, поверхности)
3) Способ проецирования параллельный ортогональный сохраняется.
Известно, что вращающаяся в плоскости, перпендикулярной оси вращения i, точка а описывает плоскую кривую – окружность. Эта окружность на одной проекции проецируется в натуральную величину, а на другой – прямой, перпендикулярной оси вращения i.
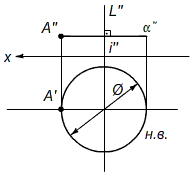
Рис. 6. – Изображение окружности в проекциях на плоскостях проекций H и V.
Задача: определить натуральную величину отрезка прямой ab (A'B';A''B'').
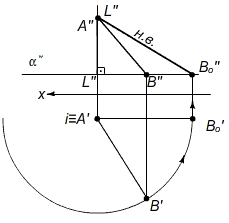
Рис. 7. – Построение натуральной величины отрезка прямой ab методом вращения вокруг фиксированной оси.
(8) Алгоритм решения:
1) Через т. А прямой ab проводим ось вращения i, перпендикулярную горизонтальной плоскости проекций. Отмечаем i (i'',i').
2) Вращением вокруг фиксированной оси i приводим отрезок прямой ab в частное положение ab||V или ab||H.
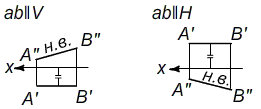
Рис. 8 – A'B'=R окружности, по которой перемещается т. B отрезка, занимая положение A'B||V.
3) Достраиваем фронтальную проекцию т. Bo'', она принадлежит плоскости кривой, перпендикулярной оси вращения i, в которой перемещается т. В.
4) Соединяем т. A''U Bo'' – полученный отрезок прямой есть натуральная величина его как прямая ab - параллельная фронтальной плоскости проекций.

