Преобразование чертежа способом замены плоскостей проекций

Метрические задачи - это задачи на определение натуральной величины отрезков прямых, углов и площадей фигур. С целью упрощения решения метрических задач применяют преобразование чертежа. Преобразование чертежа заключается в приведении геометрических образов прямых, плоскостей и др. в частное положение: параллельное плоскости проекций. Рассмотрим основные способы преобразование чертежа: I Способ замены плоскостей проекций; II Способы вращения: а) плоско-параллельное перемещение б) вращение вокруг проецирующей оси в) вращение вокруг линии уровня плоскости (вокруг горизонтали либо фронтали плоскости). Частный случай этого способа - вращение вокруг следов плоскости. Например: в плоскости ɖ, заданной следами, ɖ(ɖH, ɖV) - h''||ɖV, a h'||ɖH. Способ замены плоскостей проекций Сущность способа: 1) Геометрические образы - точки, линии, плоскости, поверхности - не изменяют свое положение в пространстве 2) Способ проецирования параллельный ортогональный сохраняется, поэтому линии A'A'' перпендикулярны оси проекций - оси х 3) Поочередно, по одной, сохраняя взаимную перпендикулярность, заменяют плоскости проекций H или V Новое положение плоскости проекций H1 или V1 выбирается параллельным геометрическому образу, т.е. чтобы привести его в частное положение. С помощью способа замены плоскостей проекций решаются 4 типовые метрические задачи: Задача I. Определить натуральную величину отрезка прямой общего положения ab; Задача II. Преобразовать отрезок прямой общего положения ab в проецирующую прямую (заданный отрезок прямой спроецировать в точку); Задача III. Преобразовать плоскость общего положения в проецирующую (заданную плоскость спроецировать в линию). Задача IV. Определить натуральную величину плоской фигуры. (3)Правило построения проекции точки А в новой системе плоскостей проекций H/V1 Дано:








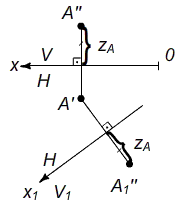
Рис. 1. Построение проекции точки в новой системе плоскостей проекций H/V1 Алгоритм решения: Допустим, что заменяется пронтальная плоскость проекций V на V1, оставаясь перпендикулярной Н. Проводим ось проекций x1. Оставляем без изменения горизонтальную плоскость проекций и горизонтальную проекцию A'. Из остающейся проекции точки A' проводим линию связи перпендикулярно оси x1, на которой от точки пересечения с осью x1 откладываем расстояние от снимаемой оси до снимаемой проекции точки (zA). Таким образом имеем две проекции точки - A' и A1'. Типовые задачи: Задача I. Дано: проекции отрезка прямой общего положения.











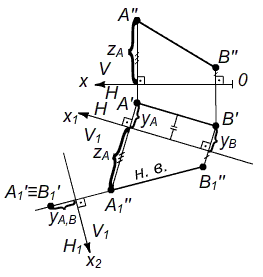
Рис. 2. Построение натуральной величины отрезка ab. Алгоритм решения: 1) Известно, что если отрезок прямой ab расположить параллельно плоскости проекций, то проекция ab на эту плоскость есть натуральная величина отрезка.




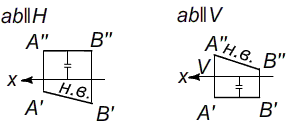
Поэтому новую ось проекций x1(V1пересекаетH=x1) проводим параллельно остающейся проекции, см. Рис. 2. (4)2) Затем достраиваем натуральную величину отрезка прямой A''B'' (см. выше "правило построения т.А в новой системе плоскостей проекции H/V1"). Задача II. Отрезок прямой ab общего положения преобразовать в проецирующее положение.











Рис. 3. Преобразование отрезка ab проецирующее положение. Алгоритм решения: 1) Известно, что если отрезок прямой ab расположен перпендикулярно плоскости проекций, то на эту плоскость он проецируется в точку, т.е. точки A≡B.





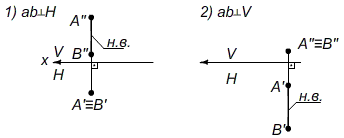
Внимание! В случаях 1) и 2) - одна проекция прямой есть точка, то другая проекция есть натуральная величина отрезка прямой ab, т.к. прямая ab расположена параллельно одной из плоскостей проекций. 2) Из вышесказанного следует, что для решения задачи II требуется сначала решить задачу I (найти натуральную величину отрезка). Т.е. необходимы две последовательные замены плоскостей проекций V→V1 и H→H1, сохраняя систему V/H взаимно перпендикулярной (линии связи A''A' и т.д. перпендикулярны оси x и x1 и x2). 3) Решение задачи II представлено на Рис. 3. (5) Задача III. Преобразовать плоскость общего положения в проецирующее положение. Задана плоскость общего положения ∆abc(A'B'C';A''B''C'')












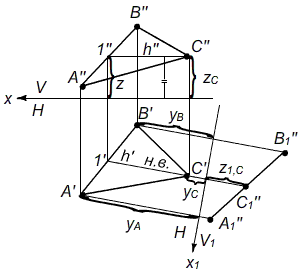
Рис. 4. Преобразование плоскости общего положения в проецирующее положение относительно плоскостей проекций H/V1. Алгоритм решения задачи III: 1) Задача решается с помощью главных линий плоскости: горизонтали h'', h' либо фронтали ее (f',f''), которые располагаются перпендикулярно оси проекций x (параллельно плоскосте проекций). На другой проеции такая прямая проецируется в точку (например, h'' или f') и соответственно плоскость треугольника - в линию.






2) На Рис. 4 представлена задача III, которая решена с помощью горизонтали h (h'',h') плоскости ∆abc. Строим h'' параллельно оси проекций x, достраиваем горизонтальную проекцию h' (по точкам C1ↄh). (6) 3) Новую плоскость V1, перпендикулярную остающейся плоскость проекций H, располагаем перпендикулярно h' (натуральная величина h) и оси x1. Тогда горизонталь h' (читай горизонтали плоскости) проецируются в точку h1'' на линии A1'B1'C1', в которую проецируется плоскость треугольника. Алгоритм решения задачи IV.















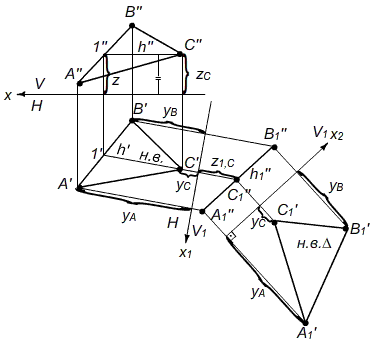
Рис. 5. Преобразование плоскости общего положения в плоскость уровня относительно системы V1/H плоскостей проекций V1/H1. 1) Сначала решают задачу III - с помощью замены одной плоскости проекций преобразуют плоскость общего положения в проецирующую, а затем располагают новую плоскость проекций параллельно линии A1''B1''C1'', которую спроецировалась плоскость треугольника.



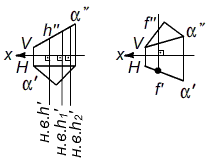
2) В новой системе плоскостей проекций от точек пересечения линий связи с осью x2 системы V1/H1 откладываем координаты yA, yB, yC для точек A1', B1', C1', соединив которые получим натуральную величину плоскости ∆abc. Таким образом, за две последовательные замены плоскостей проекций решается задача IV. Ход решения см. на Рис. 5.