Применяются 3 алгоритма для решения задач на пересечения – определение точек и линий общих для пересекающихся геометрических образов.
Алгоритм I. По этому алгоритму решаются задачи, в которых пересекаются оба проецирующие геометрические образы. В этом случае две проекции пересечения на чертеже уже есть ввиду собирательных свойств проецирующих геометрических образов.
Внимание: проецирующими поверхностями могут быть только прямые призмы и прямой круговой цилиндр.
В этом случае решение задачи сводится к умозрительному определению и обозначению двух проекций пересечения.
Задачи: построить пересечения двух геометрических образов.
а) Дано: l пересекает α (n||m) = K
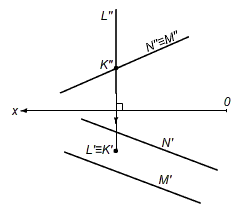
Рис. 9а. – Построение пересечения 2х геометрических образов по алгоритму I
б) Дано: α (n пересекает m) пересекает β (abc) = kt
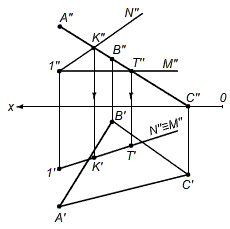
Рис. 9б. – Построение пересечения 2х геометрических образов по алгоритму I
в) Дано: α (n||m) пересекает δ = ktp
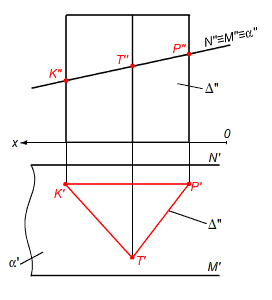
Рис. 9в. – Построение пересечения 2х геометрических образов по алгоритму I
г) Дано: θ пересекает ω = ktp, пересекаются две поверхности
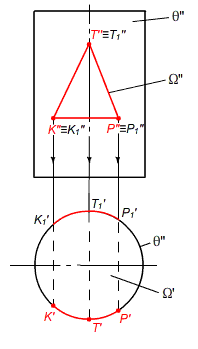
Рис. 9г. – Построение пересечения 2х геометрических образов по алгоритму I
Алгоритм II. По этому алгоритму решаются задачи на определение пересечения двух геометрических образов, из которых один – проецирующий, а другой – общего положения. В этом случае на чертеже уже есть одна проекция пересечения – на "вырожденной" проекции проецирующего геометрического образа.
Другую проекцию пересечения достраивают по признаку принадлежности точек и линий пересечения непроецирующему геометрическому образу с помощью вспомогательных прямых и окружностей.
Задача.
а) Дано: α (n пересекает m) пересекает l = K (K',K'') (1''2'' - вспомогательная прямая)
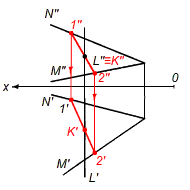
Рис. 10а. – Построение пересечения 2х геометрических образов по алгоритму II
б) Дано: поверхности δ пересекает ω = m пересекаются. Построить линию их пересечения.
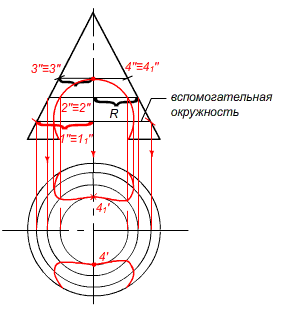
Рис. 10б. – Построение пересечения 2х геометрических образов по алгоритму II
Особые случаи пересечения. Пересечение соосных поверхностей
Две соосные (имеют общую ось вращения) поверхности пересекаются по общим для них окружностям, плоскость которых перпендикулярна оси вращения. Причем окружностей столько, сколько общих точек имеют очерковые образующие, расположенные с одной стороны от оси вращения.
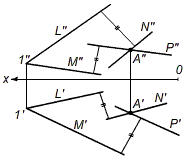
Рис. 11. – Изображение пересекающихся соосных поверхностей
(15) Способы решения задач на пересечения прямой и плоскости, прямой и поверхности, плоскости и поверхности, двух поверхностей нами обобщены. И ранее рассмотрены два алгоритма I и II для решения практических задач на пересечения геометрических образов частного положения, где проецирующими относительно плоскостей проекций являются оба пересекающихся геометрических образа (прямая, плоскость, поверхность) или - один из них.
Для решения задач, в которых пересекаются геометрические образы общего положения (непроецирующие) существует III алгоритм, который предполагает введение посредников. В качестве посредников применяют:
- вспомогательные секущие плоскости частного или общего положения,
- вспомогательные сферы – концентрические или эксцентрические.
(16) Вспомогательные плоскости выбирают такие, чтобы получить наиболее простые линии пересечения их с заданными геометрическими образами.
На рис. 12 приведено аксонометрическое изображение применения вспомогательной плоскости горизонтально-проецирующей для определения точки K пересечения прямой l с плоскостью α(треугольник abc)
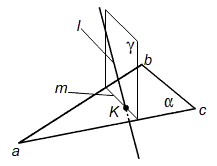
Рис. 12. – Построение точки Л пересечение l с плоскостью α.
Плоскость α (треугольник abc) пересекается с прямой l, которая заключена во вспомогательную фронтально-проецирующую плоскость γ(γV). Линия пересечения плоскостей γ и α - линия m. Так как в плоскости γ лежат две линии l и m, то их точка пересечения К очевидна. Относительная видимость определяется с помощью конкурирующих точек.
На эпюре рис. 13 представлена эта же задача.
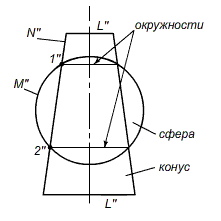
Рис. 13 – Построение точки К пересечения прямой l с плоскостью α (треугольник abc)
(17)Алгоритм III решения задач, в которых пересекаются геометрические образы общего положения. Последовательность решения:
а) выбираем вспомогательные плоскости γ1...n
б) строим линии пересечения вспомогательных плоскостей с двумя заданными поверхностями (или заданными плоскостями)
γ1 пересекает θ = m
γ1 пересекает δ = n, определяет точки пересечения m пересекает n = 1,2,3...
в) полученные точки 1,2,3... соединяем, они принадлежат линии пересечения заданных поверхностей.
Задача.
Даны поверхности: пирамида δ и сфера φ. Построить их линию пересечения.
Задачу решаем применив III алгоритм, используя посредники - вспомогательные секущие плоскости γ1...n. См. рис.14.

Рис. 14. – Построение линии пересечения поверхностей с помощью вспомогательных секущих плоскостей
Для использования в качестве посредников вспомогательных сфер необходимо остановиться на пересечении соосных поверхностей вращения.

